今日は。どのような状況なのか、全くお伝えしていなかった、TheCUIについてです。
大体出来ています。が、ディティールの作りこみが甘いです。
ですので、テスト版を某所で公開し、様子を見て、最終的に一般公開できたらと思います。
また、他に考えている案があります。今だと時期尚早ですが、「クリスマスツリー」を作ろうかと。実は昨年にも年末にiAppliで作りました。が、不出来だったので、改めて作り直そうかと思っています。
あとは、結構前から流行っている「脳トレ」に便乗したものでも作ろうかな…と。
2008年9月10日水曜日
JDBC
こんばんは。とある事情で、MySQLをJavaで扱うことになったので、ちょっとしたメモ。
JavaからMySQLを弄るために、JDBCを利用します。
JDBCとは、Javaでデータベースに接続するためのAPIです。細かい説明はすっ飛ばして、使用方法を。
MySQLは公式サイト
MySQL AB(http://www.mysql.com/)
から、ダウンロードできます。無料です。
今回は MySQL Connector/J というJDBCドライバを使いました。公式ドライバのようです。
公式サイトからDownloads -> (下の方)MySQL Connector/J とたどれば落とせます。
バージョンは5.1にしました。
落したzipを解凍。中にあるmysql-connector-java-5.1.6-bin.jarをCLASSPATHの通っているディレクトリにコピーで完了。あるいはeclipseならプロジェクト毎に、「外部JARの追加」でmysql-connector-java-5.1.6-bin.jarを追加しても出来ます。
簡単に出来ました。
JavaからMySQLを弄るために、JDBCを利用します。
JDBCとは、Javaでデータベースに接続するためのAPIです。細かい説明はすっ飛ばして、使用方法を。
MySQLは公式サイト
MySQL AB(http://www.mysql.com/)
から、ダウンロードできます。無料です。
今回は MySQL Connector/J というJDBCドライバを使いました。公式ドライバのようです。
公式サイトからDownloads -> (下の方)MySQL Connector/J とたどれば落とせます。
バージョンは5.1にしました。
落したzipを解凍。中にあるmysql-connector-java-5.1.6-bin.jarをCLASSPATHの通っているディレクトリにコピーで完了。あるいはeclipseならプロジェクト毎に、「外部JARの追加」でmysql-connector-java-5.1.6-bin.jarを追加しても出来ます。
簡単に出来ました。
2008年9月8日月曜日
画像処理 第4回 トーンカーブ
今晩は。今回は画素ごとの濃淡変換についてです。
画素ごとですので、入出力を関数で与える事が出来ます。この関数は階調変換関数と呼ばれています。そして、この関数をグラフで表したものがトーンカーブです。
入力ピクセルをx、出力ピクセルをy、階調変換関数をfとすると、次のような式になるわけです。
y = f(x)
一番簡単なのが、自分自身の写像です。
f(x)=x
グラフはFig.1に示した通りです。

Fig.1:そのまま
以降いくつか代表的なものを示します。
・折れ線型トーンカーブ
直線のみで構成される単純なトーンカーブです(Fig.2)。コントラスト調整に使われたりします。

Fig.2:折れ線型トーンカーブ
・ガンマ変換(gamma transform)
ガンマ変換は次式で表されます。
y=255*(x/255)^(1/γ)
γを変えていったときのトーンカーブをFig.3に示します。
(上からγ=3.0, 2.0, 1.5, 1.0, 0.66, 0.5, 0.33)
コントラストを調整することもできます。

Fig.3:ガンマ変換
・ネガ・ポジ反転
トーンカーブはFig.4で、入力画像と、出力画像とは濃淡が反転しています。

Fig.4:ネガポジ反転
・ソラリゼーション(solarization)
トーンカーブはFig.5。元々は写真制作時の暗室テクニックだったそうです。

Fig.5:ソラリゼーション
・擬似カラー(pseudo color)
擬似カラーはグレースケールの画像に対して施します。
RGBそれぞれでトーンカーブが異なります(Fig.6)。

Fig.6:擬似カラー
実際に画像に対しトーンカーブを適用してみます。
・ガンマ変換
サンプルは左の画像です。北海道のテレビ塔を携帯電話のカメラで撮ったものです。逆光気味で見難いです。
この画像に対しガンマ変換(γ=2.0)をかけたものが右の画像です。暗い部分のコントラストが上がって見やすくなっています。


・ソラリゼーション
サンプル画像は札幌時計台…では無く、その付近の道をカメラを揺らしながら撮影したものです。
ソラリゼーションをかけると右の画像になります。


どうなってるのか良く分からないかもです。
(ちなみに上2つの写真は、北海道旅行の際に撮ったものです。)
・擬似カラー
サンプル画像は、懲りずに「耳」です。グレースケール化しています(2値画像化はしていません)。


濃淡の若干の変化でも、色の差がよく分かります。サーモグラフィーを思い出します。
次は線形フィルタを扱えれば、と思います。
画素ごとですので、入出力を関数で与える事が出来ます。この関数は階調変換関数と呼ばれています。そして、この関数をグラフで表したものがトーンカーブです。
入力ピクセルをx、出力ピクセルをy、階調変換関数をfとすると、次のような式になるわけです。
y = f(x)
一番簡単なのが、自分自身の写像です。
f(x)=x
グラフはFig.1に示した通りです。

Fig.1:そのまま
以降いくつか代表的なものを示します。
・折れ線型トーンカーブ
直線のみで構成される単純なトーンカーブです(Fig.2)。コントラスト調整に使われたりします。

Fig.2:折れ線型トーンカーブ
・ガンマ変換(gamma transform)
ガンマ変換は次式で表されます。
y=255*(x/255)^(1/γ)
γを変えていったときのトーンカーブをFig.3に示します。
(上からγ=3.0, 2.0, 1.5, 1.0, 0.66, 0.5, 0.33)
コントラストを調整することもできます。

Fig.3:ガンマ変換
・ネガ・ポジ反転
トーンカーブはFig.4で、入力画像と、出力画像とは濃淡が反転しています。

Fig.4:ネガポジ反転
・ソラリゼーション(solarization)
トーンカーブはFig.5。元々は写真制作時の暗室テクニックだったそうです。

Fig.5:ソラリゼーション
・擬似カラー(pseudo color)
擬似カラーはグレースケールの画像に対して施します。
RGBそれぞれでトーンカーブが異なります(Fig.6)。

Fig.6:擬似カラー
実際に画像に対しトーンカーブを適用してみます。
・ガンマ変換
サンプルは左の画像です。北海道のテレビ塔を携帯電話のカメラで撮ったものです。逆光気味で見難いです。
この画像に対しガンマ変換(γ=2.0)をかけたものが右の画像です。暗い部分のコントラストが上がって見やすくなっています。


・ソラリゼーション
サンプル画像は札幌時計台…では無く、その付近の道をカメラを揺らしながら撮影したものです。
ソラリゼーションをかけると右の画像になります。


どうなってるのか良く分からないかもです。
(ちなみに上2つの写真は、北海道旅行の際に撮ったものです。)
・擬似カラー
サンプル画像は、懲りずに「耳」です。グレースケール化しています(2値画像化はしていません)。


濃淡の若干の変化でも、色の差がよく分かります。サーモグラフィーを思い出します。
次は線形フィルタを扱えれば、と思います。
2008年9月7日日曜日
画像処理 第3回 ちょっとカラーモデル
何と無くHSV変換について調べていたので、カラーモデルに関して少しばかり。
・RGB
RGB(RGBカラーモデル)は、Red、Green、Blueの3つを混ぜて色を表現する加法混色の一つです。
数値が増えるにつれて、白に近づきます。
テレビは、正にRGBカラーモデルを採用しています。モニターに近づいてドットを見ると、白のドットがRGBのドット3つで構成されているのが見えたりします。離れて見えると白に見えます、不思議。
・CMY
CMYはCyan、Magenta、Yellowの3つによる、減法混色です。
例は絵の具。数値が増えるにつれて、黒に近づきます。
この辺はよく知られていると思われます。
・HSV
HSVは色相Hue、彩度Saturation、明度Value
から構成されます。HSB(Hue、Saturation、Brightness)とも呼びます。
V=1の時の例を下に示します。

中心に向かうにつれ、白に近づいていきます。
変換式はこんな感じ。
この式だと、若干不連続な領域があります。
ちなみにJavaのColorクラスにもHSVからRGBに変換してくれるメソッドがあります。
このメソッドでは、上に示したものより不連続な点が改善されているようです。
・HLS
HLSは色相Hue、輝度Lightness/Luminance、彩度Saturation
から構成されます。 HSI(Hue、Saturation、Intensity)、HSLとも呼びます。
HSVに似ています…がちょっと違います。
L=0.5の時の例を下に示します。

中心に向かうにつれて、灰色に近づいていきます。
変換式はこんな感じ。
この変換式は、綺麗にできます。
再現性はかなり低いですが、下のようなものもあります。
I=1/5の例。

変換式は…
あまりまとまりが無いですが、こんな処で。
・RGB
RGB(RGBカラーモデル)は、Red、Green、Blueの3つを混ぜて色を表現する加法混色の一つです。
数値が増えるにつれて、白に近づきます。
テレビは、正にRGBカラーモデルを採用しています。モニターに近づいてドットを見ると、白のドットがRGBのドット3つで構成されているのが見えたりします。離れて見えると白に見えます、不思議。
・CMY
CMYはCyan、Magenta、Yellowの3つによる、減法混色です。
例は絵の具。数値が増えるにつれて、黒に近づきます。
この辺はよく知られていると思われます。
・HSV
HSVは色相Hue、彩度Saturation、明度Value
から構成されます。HSB(Hue、Saturation、Brightness)とも呼びます。
V=1の時の例を下に示します。

中心に向かうにつれ、白に近づいていきます。
変換式はこんな感じ。
h=floor(H/(PI/3))
P=I*(1-S)
Q=I*(1-S(H-h))
T=I*(1-S*(1-H+h))
if h=0 R=I, G=T, B=P
if h=1 R=Q, G=I, B=P
if h=2 R=P, G=I, B=T
if h=3 R=P, G=Q, B=I
if h=4 R=T, G=P, B=I
if h=5 R=I, G=P, B=Q
0<=R, G, B, S, I<=1, 0<=H<=2*PI
この式だと、若干不連続な領域があります。
ちなみにJavaのColorクラスにもHSVからRGBに変換してくれるメソッドがあります。
このメソッドでは、上に示したものより不連続な点が改善されているようです。
・HLS
HLSは色相Hue、輝度Lightness/Luminance、彩度Saturation
から構成されます。 HSI(Hue、Saturation、Intensity)、HSLとも呼びます。
HSVに似ています…がちょっと違います。
L=0.5の時の例を下に示します。

中心に向かうにつれて、灰色に近づいていきます。
変換式はこんな感じ。
R=X (h=H+2/3*PI)
G=X (h=H)
B=X (h=H-2/3*PI)
X(h)は下の定義
h'=h
h'=h+2*PI (h<0)
h'=h-2*PI (h>2*PI)
M2=I*(1+S) (I<=0.5)
M2=I+S-I*S (I>0.5)
M1=2*I-M2
X=M1+(M2-M1)*h'/(1/3*PI)
(h' < 1/3*PI)
X=M2
(1/3*PI <= h' < PI)
X=M1+(M2-M1)*(4/3*PI-h')/(1/3*PI)
(PI <= h' < 4/3*PI)
X=M1
(4/3*PI <= h' < 2*PI)
0<=R, G, B, S, I<=1, 0<=H<=2*PI
この変換式は、綺麗にできます。
再現性はかなり低いですが、下のようなものもあります。
I=1/5の例。

変換式は…
R=I/3+2*S*cosH
G=I/3-S*cosH+S*sinH
B=I/3-S*cosH-S*sinH
0<=R, G, B<=1, 0<=I<=3, 0<=H<=2*PI, 0<=S<=2/3
あまりまとまりが無いですが、こんな処で。
2008年9月4日木曜日
画像処理 第1回 補間
こんばんは。
ネタが溜まってきました。
さて最近凝っているネタがデジタル画像処理です。画像なので、処理結果が眼で確認できて、非常に分かりやすいです。今回は、「補間」についてです。
「補間」は画像の再標本化の時に使われます。よくある例が拡大です。デジタル画像では座標が離散値ですが、拡大する際には、小数値のピクセルが欲しくなります。で、小数値のピクセルを計算でなんとか求めようというわけです。
主に3つの方法があります。
・ニアレストネイバー(nearest neighbor)
もっとも単純な補間法です。
座標(x,y)のピクセル値I(x,y)は次の式で与えられます(fは元画像のピクセル)。
I(x,y) = f([x+0.5],[y+0.5])
・バイリニア補間(bilinear interpolation)
こちらは次のような式であらわされます(括弧は行列を表しています)。対象のドットに近い周囲4ドットを用いています。
ニアレストネイバーをしてから、平均化したような感じです。
・バイキュービック補間(bicubic interpolation)
3つの中で最も効果の大きい補間方法です。
式は次の通り。対象のドットに近い周囲16ドットを用いています。
関数h(t)は、sinc関数(sinc(t)=sin(πt)/(πt))を3次多項式で近似したもので次式で表されます。
では、これらの補間を実際に施した画像を見てみましょう。
画像はFig.1にしめしたもので、「あ」の文字です。サイズ24のHGS行書体です。
この画像をそれぞれ20倍に拡大したものを以下に示します。
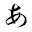
Fig.1:元画像
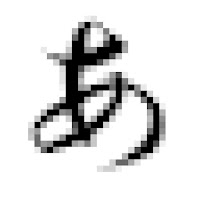
Fig.2:ニアレストネイバー
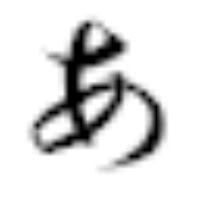
Fig.3:バイリニア補間
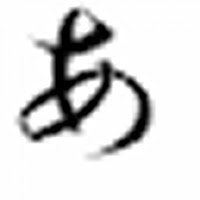
Fig.4バイキュービック補間
Fig.2は非常にジャギが目立ちます。
Fig.3は平滑化の効果から、ジャギは目立たなくなりますが、エッジが鈍っています。
Fig.4は全体的にFig.3よりスマートに見えます。先端部分も上手く再現されていて、自然な画像となっています。
では今回はこの辺で。次回は、線形フィルタ全般を扱えればと思います。
ネタが溜まってきました。
さて最近凝っているネタがデジタル画像処理です。画像なので、処理結果が眼で確認できて、非常に分かりやすいです。今回は、「補間」についてです。
「補間」は画像の再標本化の時に使われます。よくある例が拡大です。デジタル画像では座標が離散値ですが、拡大する際には、小数値のピクセルが欲しくなります。で、小数値のピクセルを計算でなんとか求めようというわけです。
主に3つの方法があります。
・ニアレストネイバー(nearest neighbor)
もっとも単純な補間法です。
座標(x,y)のピクセル値I(x,y)は次の式で与えられます(fは元画像のピクセル)。
I(x,y) = f([x+0.5],[y+0.5])
・バイリニア補間(bilinear interpolation)
こちらは次のような式であらわされます(括弧は行列を表しています)。対象のドットに近い周囲4ドットを用いています。
ニアレストネイバーをしてから、平均化したような感じです。
| I(x, y) = | ( | [x]+1-x | x-[x] | ) | ( | f([x], [y]) | f([x], [y]+1) | ) | ( | [y]+1-y | ) |
| f([x]+1, [y]) | f([x]+1, [y]+1) | y-[y] |
・バイキュービック補間(bicubic interpolation)
3つの中で最も効果の大きい補間方法です。
式は次の通り。対象のドットに近い周囲16ドットを用いています。
| I(x, y) = | ( | h(x1) | h(x2) | h(x3) | h(x4) | ) | ( | f11 | f12 | f13 | f14 | ) | ( | h(y1) | ) |
| f21 | f22 | f23 | f24 | h(y2) | |||||||||||
| f31 | f32 | f33 | f34 | h(y3) | |||||||||||
| f41 | f42 | f43 | f44 | h(y4) |
関数h(t)は、sinc関数(sinc(t)=sin(πt)/(πt))を3次多項式で近似したもので次式で表されます。
| h(t) = | { | |t|^3-2|t|^2+1 | (|t|<=1) |
| -|t|^3+5|t|^2-8|t|+4 | (1<|t|<=2) | ||
| 0 | (2<|t|) |
では、これらの補間を実際に施した画像を見てみましょう。
画像はFig.1にしめしたもので、「あ」の文字です。サイズ24のHGS行書体です。
この画像をそれぞれ20倍に拡大したものを以下に示します。
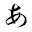
Fig.1:元画像
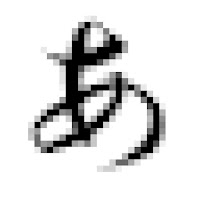
Fig.2:ニアレストネイバー
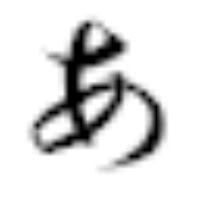
Fig.3:バイリニア補間
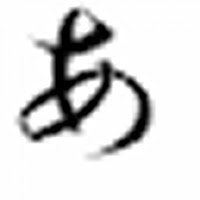
Fig.4バイキュービック補間
Fig.2は非常にジャギが目立ちます。
Fig.3は平滑化の効果から、ジャギは目立たなくなりますが、エッジが鈍っています。
Fig.4は全体的にFig.3よりスマートに見えます。先端部分も上手く再現されていて、自然な画像となっています。
では今回はこの辺で。次回は、線形フィルタ全般を扱えればと思います。
登録:
コメント (Atom)
