画像処理 第1回 補間

こんばんは。
ネタが溜まってきました。

さて最近凝っているネタがデジタル画像処理です。画像なので、処理結果が眼で確認できて、非常に分かりやすいです。今回は、「補間」についてです。

「補間」は画像の再標本化の時に使われます。よくある例が拡大です。デジタル画像では座標が離散値ですが、拡大する際には、小数値のピクセルが欲しくなります。で、小数値のピクセルを計算でなんとか求めようというわけです。

主に3つの方法があります。

・ニアレストネイバー(nearest neighbor)
もっとも単純な補間法です。
座標(x,y)のピクセル値I(x,y)は次の式で与えられます(fは元画像のピクセル)。

I(x,y) = f([x+0.5],[y+0.5])

・バイリニア補間(bilinear interpolation)
こちらは次のような式であらわされます(括弧は行列を表しています)。対象のドットに近い周囲4ドットを用いています。
ニアレストネイバーをしてから、平均化したような感じです。

I(x, y) =	(	[x]+1-x	x-[x]	)	(	f([x], [y])	f([x], [y]+1)	)	(	[y]+1-y	)
						f([x]+1, [y])	f([x]+1, [y]+1)			y-[y]

・バイキュービック補間(bicubic interpolation)
3つの中で最も効果の大きい補間方法です。
式は次の通り。対象のドットに近い周囲16ドットを用いています。

I(x, y) =

(

h(x1)

h(x2)

h(x3)

h(x4)

)

(

f11

f12

f13

f14

)

(

h(y1)

)

f21

f22

f23

f24

h(y2)

f31

f32

f33

f34

h(y3)

f41

f42

f43

f44

h(y4)

関数h(t)は、sinc関数(sinc(t)=sin(πt)/(πt))を3次多項式で近似したもので次式で表されます。

h(t) =	{	|t|^3-2|t|^2+1	(|t|<=1)
		-|t|^3+5|t|^2-8|t|+4	(1<|t|<=2)
		0	(2<|t|)

では、これらの補間を実際に施した画像を見てみましょう。
画像はFig.1にしめしたもので、「あ」の文字です。サイズ24のHGS行書体です。
この画像をそれぞれ20倍に拡大したものを以下に示します。

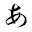
Fig.1:元画像


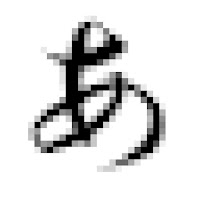
Fig.2:ニアレストネイバー


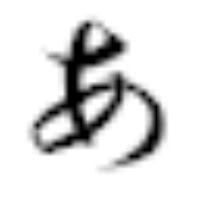
Fig.3:バイリニア補間


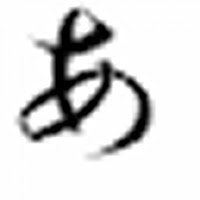
Fig.4バイキュービック補間

Fig.2は非常にジャギが目立ちます。
Fig.3は平滑化の効果から、ジャギは目立たなくなりますが、エッジが鈍っています。
Fig.4は全体的にFig.3よりスマートに見えます。先端部分も上手く再現されていて、自然な画像となっています。

では今回はこの辺で。次回は、線形フィルタ全般を扱えればと思います。