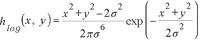先日の2値化では,ある閾値を設け,それより画素値が高いか否かで白黒判断していました.
しかし,それだと満足しない方もおられるはず.
というわけで,ハーフトーニング.渇いた喉を潤してくれます.
簡単に言うと,白黒の2値だけで,濃淡の微妙な変化を表現しようというものです.
スクリーントーンとかは正にそれです.
・濃度パターン法(density pattern method)
1つのグレースケール画素を複数の2値画像で表現します.
例えば,1画素を4x4画素の2値画像で表現するとすると,256階調を17分割することができます.

Fig.1
こんな感じ.
1画素を4x4画素で表現するので,入力画像がWxH画素の場合,出力画像4Wx4H画素となります.
・ディザ法(dither method)
ディザパターンというものを使う方法です.

Fig.2 Dither pattern
1. 入力画像を4x4のブロックに分割する.
2. ブロック内の各画素がディザパターンの対応画素*16+8以上なら,出力画素を255,そうでないなら,0とする.
3. 全てのブロックについて,2を行う.
ディザ法では周期的パターンが目立つので(実例を後述します),ディザパターンをFig.2に固定せず,可変にする方法も考案されているようです.
・誤差拡散法(error diffusion method)
これは,2値化を行うことによる誤差をキャンセルさせて行くというものです.
処理の流れは,以下の通り.
f:入力画素
g:出力画素
1. fからgを以下の様に決定し,誤差をe=g-fとする.
f>127 → g=255
f≦128 → g=0
2. 誤差eを入力画素周辺の数画素に分散させる.
分散式の例:
f=f(x, y)だったとき
f'(x+1, y)=f(x+1, y)+(5/16)e
f'(x+1, y)=f(x-1, y+1)+(3/16)e
f'(x+1, y)=f(x, y+1)+(5/16)e
f'(x+1, y)=f(x+1, y+1)+(3/16)e
3. 1,2の処理を,全画素について行う(左上から右下に向かって).
下が今回の例.

Fig.3 sample

Fig.4 density pattern method
出力画像がでかいので一部のみ.

Fig.5 dither method

Fig.6 error diffusion method
誤差拡散法が一番周期的パターンが目立ちにくいです.
これでまた一つ,人生の楽しみが増えました.