画像処理 第5回 線形フィルタ

こんばんは。とてつもない間がありましたが、気にしない方向で。
…今回は線形フィルタについてです。

画像処理の中で、領域に基づく濃淡変換を空間フィルタリングと呼んでいます。で、そこで用いられるフィルタを空間フィルタと呼んでいます。そして更に、空間フィルタは線形フィルタと、非線形フィルタに分けられます。今回紹介する線形フィルタは次式で表されます。



f(x, y)は入力、g(x, y)は出力、h(m, n)はフィルタの係数。
フィルタの大きさは(2w+1)*(2w+1)です。w=1、つまり3*3のフィルタは次のようになっているわけです。

Tab.1 線形フィルタ

h(-1, -1)	h(0, -1)	h(1, -1)
h(-1, 0)	h(0, 0)	h(1, 0)
h(-1, 1)	h(0, 1)	h(1, 1)

というわけで、いくつかのフィルタを紹介します。

・平均化フィルタ(averaging filter)
非常にシンプルなフィルタです。やることは平滑化、つまり、画像をぼかします。
フィルタは次の表です。

Tab.2 平均化フィルタ(3*3)

1/9	1/9	1/9
1/9	1/9	1/9
1/9	1/9	1/9

Tab.3 平均化フィルタ(5*5)

1/25	1/25	1/25	1/25	1/25
1/25	1/25	1/25	1/25	1/25
1/25	1/25	1/25	1/25	1/25
1/25	1/25	1/25	1/25	1/25
1/25	1/25	1/25	1/25	1/25

・加重平均化フィルタ(weighted averaging filter)
平均化フィルタではありますが、重みが付いています。
中央ほど重みが強いので、先の平均化フィルタに比べエッジが残りやすいという特徴があります。

Tab.4 加重平均化フィルタ(3*3)

1/16	2/16	1/16
2/16	4/16	2/16
1/16	2/16	1/16

Tab.5 加重平均化フィルタ(5*5)

1/256	4/256	6/256	4/256	1/256
4/256	16/256	24/256	16/256	4/256
6/256	24/256	36/256	24/256	6/256
4/256	16/256	24/256	16/256	4/256
1/256	4/256	6/256	4/256	1/256

・ガウシアンフィルタ(Gaussian filter)
ガウス分布に従った加重平均化フィルタ。
ガウス分布は以下の式です。



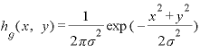
・微分フィルタ
離散値だけど微分。
⊿f(x)=f(x)-f(x-1)
みたいなノリです。いくつかパターンがあるので示しておきます。また、方向も横、縦とあります。
簡単にいえば、このフィルタではエッジ検出が出来ます。しかし、ノイズに敏感だったりします。

Tab.6 微分フィルタ(横方向1)

0	0	0
0	-1	1
0	0	0

Tab.7 微分フィルタ(横方向2)

0	0	0
-1	1	0
0	0	0

Tab.8 微分フィルタ(横方向3)

0	0	0
-1/2	0	1/2
0	0	0

Tab.9 微分フィルタ(縦方向1)

0	1	0
0	-1	0
0	0	0

Tab.10 微分フィルタ(縦方向2)

0	0	0
0	1	0
0	-1	0

Tab.11 微分フィルタ(縦方向3)

0	1/2	0
0	0	0
0	-1/2	0

・プリューイットフィルタ(Prewitt filter)
プリューイットフィルタは横(縦)方向に微分した後、縦(横)方向に平滑化します。つまり、先の微分フィルタに比べ、ノイズが低減されるということです。

Tab.12 プリューイットフィルタ(横方向)

-1	0	1
-1	0	1
-1	0	1

Tab.13 プリューイットフィルタ(縦方向)

1	1	1
0	0	0
-1	-1	-1

・ソーベルフィルタ(Sobel filter)
このフィルタは、大体プリューイットフィルタと同じですが、平滑化の際、中央に重みを付けています。

Tab.14 ソーベルフィルタ(横方向)

-1	0	1
-2	0	2
-1	0	1

Tab.15 ソーベルフィルタ(縦方向)

1	2	1
0	0	0
-1	-2	-1

・2次微分フィルタ
その名の通り、離散値だけど2次微分します。微分フィルタ1の出力から、微分フィルタ2の出力を引くと、丁度2次微分になります。

Tab.16 2次微分フィルタ(横方向)

0	0	0
1	-2	1
0	0	0

Tab.17 2次微分フィルタ(縦方向)

0	1	0
0	-2	0
0	1	0

・ラプラシアンフィルタ(Laplacian filter)
このフィルタは、縦横方向の2次微分の結果を足し合わせたものです。方向に依存しないエッジが得られます。

Tab.18 ラプラシアンフィルタ

0	1	0
1	-4	1
0	1	0

・鮮鋭化フィルタ(sharpening filter)
このフィルタは入力画像からラプラシアンフィルタの出力を引いたものです。このフィルタを掛けると、エッジが強調されます。(鮮鋭化フィルタ2は、入力画像からラプラシアンフィルタを変形したものを引いています。)

Tab.19 鮮鋭化フィルタ1

0	-1	0
-1	5	-1
0	-1	0

Tab.20 鮮鋭化フィルタ2

-1	-1	-1
-1	9	-1
-1	-1	-1

では、これらのフィルタをサンプル画像に施してみます…と思ったのですが、投稿が長くなってしまったので、実際の例は次回へと回そうと思います。